Dimensions and section properties for W5X19
Structural sectional properties for a W5X19 standard steel section
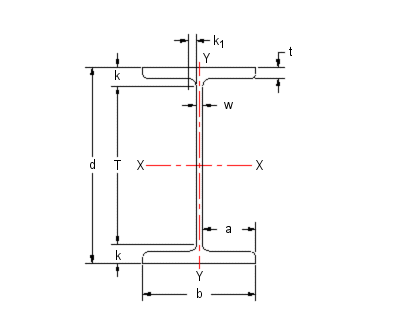
US Customary Units
| Description | Symbol | Value |
|---|---|---|
| Shape Category / Designation | Type | W |
| Section Name | Name | W5X19 |
| Cross Sectional Area | A | 5.56 in2 |
| Section Width | b | 5.03 in |
| Section Depth | d | 5.15 in |
| Flange thickness | tf | 0.43 in |
| Web thickness | tw | 0.27 in |
| Radius of Gyration about X-X | rx | 2.17 in |
| Radius of Gyrations about Y-Y | ry | 1.28 in |
| Moment of Inertia about X-X | Ix | 26.3 in4 |
| Moment of Intertia about Y-Y | Iy | 9.13 in4 |
| Elastic Section Modulus about X-X | Sx | 10.2 in3 |
| Elastic Section Modulus about Y-Y | Sy | 3.63 in3 |
| Plastic Section Modulus about X-X | Zx | 11.6 in3 |
| Plastic Section Modulus about Y-Y | Zy | 5.53 in3 |
| St. Venant Torsional Constant | J | 0.316 in4 |
| Warping Torsion Constant | Cw | 50.9 in6 |
| Self Weight of section | Weight | 19 lb/ft |
Metric Units
| Description | Symbol | Value |
|---|---|---|
| Shape Category / Designation | Type | W |
| Section Name | Name | W5X19 |
| Cross Sectional Area | A | 3587 mm2 |
| Section Width | b | 128 mm |
| Section Depth | d | 131 mm |
| Flange thickness | tf | 10.9 mm |
| Web thickness | tw | 6.9 mm |
| Radius of Gyration about X-X | rx | 55 mm |
| Radius of Gyrations about Y-Y | ry | 33 mm |
| Moment of Inertia about X-X | Ix | 11000000 mm4 |
| Moment of Intertia about Y-Y | Iy | 4000000 mm4 |
| Elastic Section Modulus about X-X | Sx | 167000 mm3 |
| Elastic Section Modulus about Y-Y | Sy | 59000 mm3 |
| Plastic Section Modulus about X-X | Zx | 190000 mm3 |
| Plastic Section Modulus about Y-Y | Zy | 91000 mm3 |
| St. Venant Torsional Constant | J | 132000 mm4 |
| Warping Torsion Constant | Cw | 14000000000 mm6 |
| Self Weight of section | Weight | 28 kg/m |
Note: Metric units have been converted from tabulated imperial values and rounded to a reasonable number of significant figures.
A W5X19 steel section is a standard North American steel section in the W - Wide Flange category. The height and width of the section are 5.15 in (131 mm) and 5.03 in (128 mm) respectively. It weighs 19 lb/ft (28 kg/m) and has a cross sectional area of 5.56 in2 (3587 mm2).
The section has a tensile yield capacity of:
kip
The section has a flexural plastic moment capacity of:
kip-ft
The section has a flexural elastic moment capacity of:
kip-ft